Insights
Solving the Problem with Word Problems, Part II Addition & Subtraction
Whether you teach first grade, third grade, or sixth grade, your students will be working word problems (lots of word problems) as a way to learn mathematical concepts. As students move through the grades, the word problems become progressively more difficult, the class of numbers changes from whole numbers to fractions, decimals, and integers, and the concepts are more complex but the underlying structure of the word problem in many ways remains the same. In this post we are going to look at addition and subtraction and the full range of jobs these two operations help us perform mathematically.
Let’s Start with the Five Representations
Every time we interact with math, we are going to use one or more of the five representations in the image below.
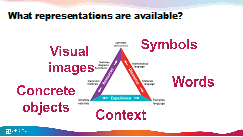
But all too often we ask kids to jump right from reading the word problem to writing out a symbolic equation. To help students truly make sense of what’s going on in a particular word problem, we need to slow down and spend time in what I refer to as the mathematical sand box, which I discussed at length in the previous post on word problems. Instead of using buckets and shovels as they would in a real sandbox, students may be using fraction pieces, base-10 blocks, counters, or drawings. The tools they use will depend on the specific question being asked. The important thing is when students are layering context with multiple representations, they are building critical comprehension of the math concepts underlying the word problem.
What Is the Work of Addition & Subtraction
When we think about addition and subtraction, we know that they are operations that students focus on using whole numbers in the primary grades, greater whole numbers in the intermediate grades, and fractions and decimals in the upper elementary and middle grades. But add and subtract (as well as multiply and divide) also do specific jobs. The work of addition and subtraction can be split into situations—active and relationship—and this remains true no matter how complex the numbers, the language, or the concepts presented in any word problem solved by adding or subtracting.
Let’s look at the following two problems.
Problem A
There are 26 students in Mrs. Amadi’s class. 15 left to get ready to play in band at the assembly. How many students remain in the classroom?
Problem B
There are 26 students in Mrs. Amadi’s class. 15 play on the concert band. The rest sing the in the choir. How many are in the choir?
In problem A, an action is involved, 15 students left the classroom. And for younger students, it’s often easier to see that problem A involves subtraction. But in problem B no students came into the classroom and no students left the classroom. Problem B involves a relationship between groups and it’s not as clear what operation to use when solving problem B. Let’s explore in greater depth what active and relationship situations look like with addition and subtraction.
Active Situations
When something comes in we use addition, when something goes out we use subtraction. And this isn’t about searching for keywords, which not only don’t help kids understand the math behind the words, but also don’t help students with real-world problems where the language may not be as friendly. Rather we want students to understand what action each operation performs. In the case of addition something comes in, five cars drove into the parking lot, three students joined the team, or I clipped five pages to a stack of twelve. In the case of subtraction something goes away, three birds flew off, I ate five cookies, or I spent five of eleven quarters.
Furthermore, we can vary these active situations by changing the missing piece or the part that’s unknown. In essence, word problems are like a short story, they have a beginning (starting value), a middle (change value), and an end (resulting value). The following word problem illustrates variations on an active situation where the missing value changes.
| ACTIVE SITUATION | ||
| Result Unknown | Change Addend Unknown | Start Addend Unknown |
| There are 26 students in Mrs. Amadi class. After lunch, 15 left to get ready to play in the band at assembly. How many students are not in the band?
26-15=x 26=15 +x |
There are 26 students in Mrs. Amadi’s class. After the band students left the classroom for assembly, there were 11 students still in the classroom. How many students are in the band?
26-x=11 x+11=26 |
After lunch, 15 band students left Mrs. Amadi’s class to get to ready to play in the assembly. There were 11 students still in the classroom. How many students are in Mrs. Amadi’s classroom?
x-15=11 15+11=x |
Relationship Situations
Addition and subtraction also help us with the work of relationships, (1) where a total is separated into groups or parts—what we refer to as part-part-whole—or (2) when two quantities have a constant difference—what we refer to as additive comparison. And as with active situations involving addition and subtraction, relationship situations can also vary by the missing value, what part of the story remains unknown. In the case of part-part-whole problems, the total, one part, or both parts could be unknown. In the case of additive comparison, the difference, the greater quantity, or the lesser quantity is unknown.
| RELATIONSHIP SITUATION- Part-Part-Whole | ||
| Total Unknown | One Part Unknown | Both Parts Unknown |
| The 4th grade voted to decide where to go for the annual field trip. 32 students voted to go to the ice-skating rink. 63 students voted to go to the local park. How many students are in the 4th grade?
32+63=x x-63=32 |
The 4th grade voted to decide where the 95 students should go for their annual field trip. 32 students voted to go to the ice-skating rink. The rest chose the local park. How many students voted to go to the park?
32+x=95 x=95-32 |
The 4th grade voted to decide where the 95 students in the grade should for their annual field trip. Some students voted to go to the ice-skating rink, others voted to go to the local park. What are some of the possible combinations of votes?
x+y=95 95-x=y
|
| Additive Comparison | ||
| Difference Unknown | Greater Quantity Unknown | Lesser Quantity Unknown |
| Jessie and Roberto both collect baseball cards. Roberto has 53 cards and Jessie has 71 cards. How many fewer cards does Roberto have than Jessie?
53+x=71 71-53=x |
Jessie and Roberto both collect baseball cards. Roberto has 53 cards and Jessie has 18 more than Roberto. How many baseball cards does Jessie have?
32+x=95 x=95-32 |
Jessie and Robert both collect baseball cards. Jessie has 71 cards. Roberto has 18 fewer cards than Jessie. How many baseball cards does Roberto have?
x+y=95 95-x=y |
Students should progressively encounter all of these types of addition and subtraction word problems in kindergarten through second grade. What we find however, is that even in first and second grades, students are mostly still working with the types of word problems introduced in kindergarten. So, when in real life or on a high-stakes test, students come across an additive comparison problem or an active situation where the start addend is unknown, they feel like it’s a trick question and don’t know how to approach it.
That’s why playing in the math sandbox, understanding the context of the problem, using concrete objects or drawings to make sense of the situation is so critical. Because it’s at this stage that students see the relationship between addition and subtraction, explore a variety of strategies, discover that some approaches are more efficient for certain problems, and most important can translate this understanding to other mathematical situations. In other words, they develop operation sense that they can use to solve progressively more difficult problems involving addition and operation. So, as they move into the upper elementary grades and encounter fractions and decimals, they recognize the underlying structure of the word problem. Is it an active or relationship problem? What is the unknown? What strategies might they use to grapple with the problem? And what operation will help them most efficiently reach a solution?




