Cal's Corner
Greedy Algorithims
The word ‘algorithm’ is well known today. It is over 1,000 years old and comes from the name of a middle eastern mathematician who devised many step-by-step procedures for working with numbers. Today there are all types of algorithms and, to promote thinking, we should encourage students to devise their own methods.
During a recent study session, we were working with subtraction of mixed numbers – which can be very messy. The word problem suggests this subtraction equation.

After rewriting the fractions so the denominators were the same, my students were left with:
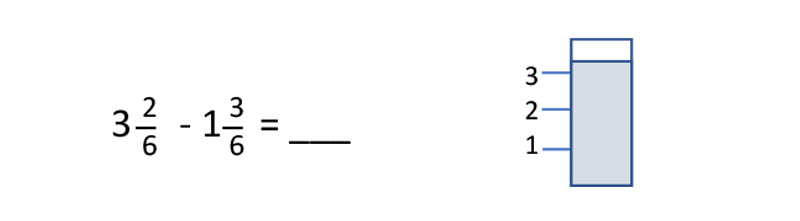
Various methods were used for the next step. Interestingly, one student chose to break the fraction in the subtrahend into two parts to subtract.
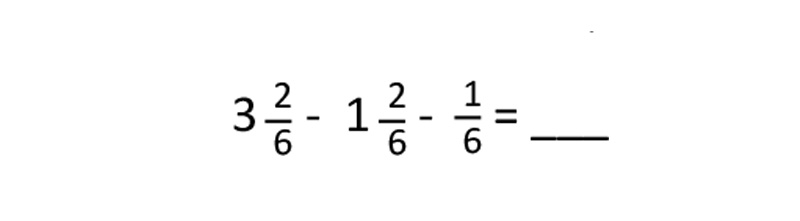
The student then drew an arrow to show the subtraction of the first fraction and that 2 cups would remain. The next step was to subtract the second fraction from 2 cups and simply write the answer.
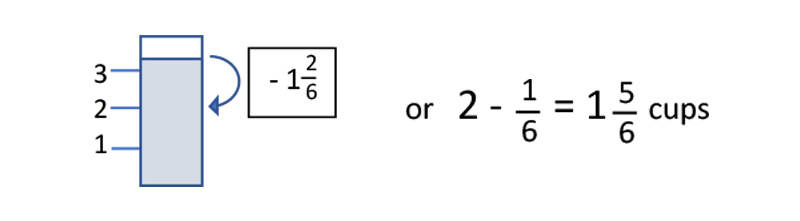
Clever, but was this a fluke? The student proceeded to complete every example the same way when the fraction in the subtrahend was greater than the minuend and then showed me the same approach with whole numbers. For example,
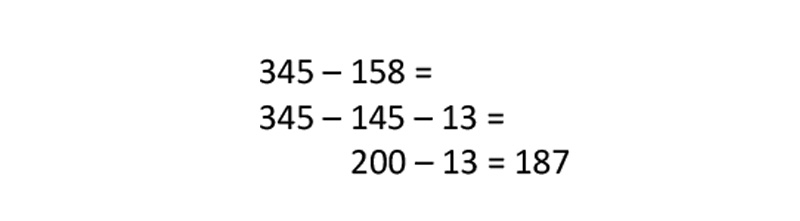
I wondered – could this be a good algorithm? After trying a few more examples, my student did share the fact that there were other methods used with “different” numbers. This meant these steps work best when the fraction part of mixed numbers or the tens/ones parts of whole numbers were about the same. It was true the steps above would always work, but they were not that easy to do in your head when there were other number combinations.
The methods like the example above are sometimes today called greedy algorithms because they are easy to use in some situations, do achieve a solution, but may not be the most efficient in all situations. These are sometimes the types of techniques employed by individuals who write instructions for a computer to follow. The steps work, but they may not always be the most efficient. In the age of technology; efficiency hasn’t always been important. When a machine is performing the instructions, who really cares how long it takes. No matter what, it will be fast!
Today, work with computational thinking in the classroom is structured to encourage students to create and explore all types algorithms. We know that some algorithms are better and others, but at this stage, it is the experience with a range of algorithms that is important. We should explore more algorithms like those my Year 6 student suggested. Does it work for all subtraction situations involving fractions? Does it work for all numbers?
Here are some examples for you to try. You might want to discuss these with colleagues and/or students.
1. Find the difference between these two prices.
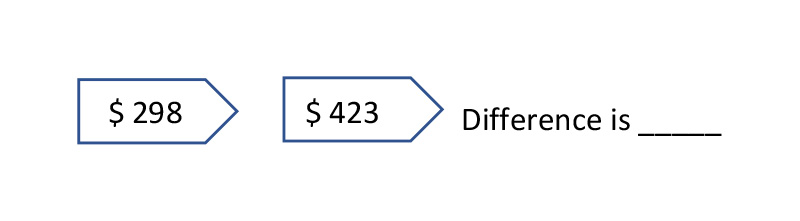
What method(s) did you use?

2. Repeat the steps for this pair of prices.

How did you think? Was it similar to the first example?

3. Write two other 3-digit prices.
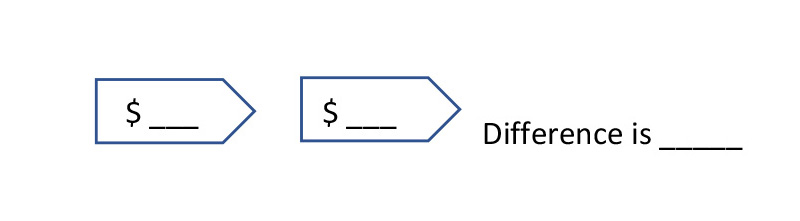
Find the difference.
In what way(s) was your thinking the same as the examples above? How was your thinking different from the other methods you used?

Footnote: At one time, it was true that very little concern was given to writing efficient computer algorithms. That view has changed. Today, the goal is to write elegant algorithms without being greedy!




